domingo, 4 de setembro de 2011
Mais um trabalhinho da Ana Filipa...
... que merece uma grande salva de palmas porque fez este trabalho fantástico, mesmo estando de férias!
segunda-feira, 1 de agosto de 2011
O fantástico jogo do semáforo da Ana Filipa e da Diana:
Já todos ouvimos falar de campeonatos de jogos matemáticos. Ao contrário do que possas pensar, estes jogos são mais do que a matemática que conhecemos. Podes construir e jogar alguns dos jogos dos campeonatos de matemática.
Primeiro
Segundo:
Terceiro
Quarto:
Quinto:
Sexto:
Sétimo:
Oitavo:
Nono:
Parabéns, minhas queridas, o jogo ficou fantástico!!
domingo, 3 de julho de 2011
domingo, 26 de junho de 2011
À Descoberta da Matemática
Jonh, é um homem solteiro que viaja à descoberta da Matemática pelo Mundo. Só que as viagens dele não eram normais. Jonh... viajava no tempo.
Um dia foi até ao Egipto, e para o receber, estavam Mamadeu e Xangu, à sua espera no Portal Mágico da História da Matemática. E levaram-no até à tribo Judá. Isto, no século XV a.C.
Jonh conheceu toda a tribo. Adormeceu, para no dia seguinte, ir à descoberta da Matemática.
De manhã, ajudou Xangu a contar as ovelhas, com paus. Por exemplo, no dia anterior, tinha 11 paus, e se no dia seguinte tivessem apenas 10 paus, era sinal que faltava 10 ovelhas.
Ao meio-dia, foram almoçar. Depois, foram à procura de comida para ajudar nas tarefas da tribo, mas Jonh encontrou um papel. Olhou-o mais de perto e reconheceu-o: era o Papiro de Rhind! Só que Jonh nunca pensara ser ele a encontrá-lo!
De noite, Jonh e os da tribo estiveram a contar histórias sobre animais. Os da tribo estiveram, com a ajuda de John, a desenhar figuras na areia. Eles atribuíram números a cada figura.
Entretanto, descobriram que, afinal, o Papiro de Rhind tinha um compartimento secreto, onde estavam guardadas há séculos as indicações de um tesouro. Jonh tinha espírito aventureiro e, por isso, foi logo ter com o Mamadeu, para o ajudar a decifrar as indicações do mistério. Mamadeu descobriu que era um mapa do tesouro, e que o tesouro estava escondido numa das pirâmides. Mamadeu fez questão que, se ele não fosse, pelo menos, o ajudante, Xangu tinha de ir.
Então, lá foram eles à busca do tesouro. Foram a correr.
Quando chegaram à pirâmide, repararam que, em cada lado, havia uma numeração diferente. As numerações eram: babilónica, romana maia e egípcia.
De baixo de cada numeração, haviam portas, três más e uma boa. Para que Jonh não ficasse ferido, abriu logo todas as portas. Na babilónica apareceu uma múmia, na romana apareceram morcegos, na maia apareceu um esqueleto e na egípcia apareceu o Papiro de Moscovo que era a chave para voltar ao presente.
De repente, Jonh é acordado pela mãe. Será que foi tudo um sonho?
Papiro de Rhind: 1650 a.C Papiro de Moscovo: 1890 a.C.
Parabéns Beatriz, Ema, Laura, Margarida, Sofia!!
terça-feira, 3 de maio de 2011
quarta-feira, 27 de abril de 2011
Os sólidos da Ema...
Cone, cilindro, pirâmide quadrangular, prisma triangular, prisma rectangular, cubo.
Os sólidos do Eduardo...
Cilindro, pirâmide quadrangular, prisma rectangular, prisma triangular, cone, cubo.
Os sólidos do Filipe...
Cone, pirâmide quadrangular, cilindro, cubo, prisma triangular, prisma rectangular.
Os sólidos da Ana Catarina...
Cilindro, pirâmide hexagonal, cubo, pirâmide triangular, prisma rectangular, prisma pentagonal.
Os sólidos da Diana...
Cilindro, prisma rectangular, pirâmide hexagonal, prisma pentagonal, pirâmide triangular, cubo.
Sólidos Platónicos - Trabalho do Eduardo
INTRODUÇÃO
Neste trabalho vou falar nos Sólidos Platónicos, referindo as características de cada um.
Platónicos são sólidos formados por polígonos geometricamente iguais, tendo como sua referencia o filósofo Platão acerca de 350 a.C.
TETRAEDO
CUBO
(hexaedro)
O cubo é o único poliedro regular com faces quadrangulares. O cubo tem 6 faces, pelo que também se pode chamar de hexaedro (hesa significa seis em grego).
Este sólido representa a terra, porque Platão acreditava e afirmava que os átomos de terra seriam cubos, os quais permitiam ser colocados perfeitamente lado a lado, conferindo-lhes solidez.
OCTAEDRO
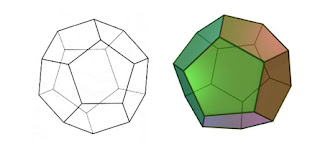
DODECAEDRO
ICOSAEDRO
CONCLUSÃO
Bibliografia
I. http://pt.wikipedia.org
II. http://avrinc05.no.sapo.pt/
Neste trabalho vou falar nos Sólidos Platónicos, referindo as características de cada um.
Platónicos são sólidos formados por polígonos geometricamente iguais, tendo como sua referencia o filósofo Platão acerca de 350 a.C.
TETRAEDO
O tetraedro regular é um sólido platónico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros possui 4 vértices, 4 faces e 6 arestas. Considerado como um caso particular de pirâmide regular de base triangular, o volume do tetraedro regular é dado pela expressão matemática.
O filósofo grego Platão estabelecia uma ligação dos poliedros com as forças da natureza, hoje podemos estudar as formas moleculares existentes na natureza e observarmos que as ideias que Platão teve por volta do século V e IV a.C. são verificadas e comprovadas.
CUBO
(hexaedro)
O cubo é o único poliedro regular com faces quadrangulares. O cubo tem 6 faces, pelo que também se pode chamar de hexaedro (hesa significa seis em grego).
Este sólido representa a terra, porque Platão acreditava e afirmava que os átomos de terra seriam cubos, os quais permitiam ser colocados perfeitamente lado a lado, conferindo-lhes solidez.
OCTAEDRO
O octaedro é um poliedro regular ou sólido platónico. Platão era um filósofo e matemático grego que acabou por se tornar num dos pensadores mais influentes do pensamento ocidental. Nascido em Atenas, cerca de 427 a.C., foi discípulo de Sócrates e uma das ideias que a sua escola de pensamento afirmava era que toda a matéria era constituída por quatro elementos, sendo cada um deles representado por um sólido geométrico regular. Deste modo, fazia corresponder à Terra o cubo, ao Fogo o tetraedro, ao Ar o octaedro e à Água o icosaedro. O dodecaedro foi considerado por Platão como o símbolo do Universo.
DODECAEDRO
O mais harmonioso e soberano dos sólidos Platónicos é o dodecaedro que, segundo Platão, representa o universo ou o cosmos. É constituído por doze pentágonos e não se divide em outros poliedros regulares. Possui 30 arestas, 20 vértices e 12 faces pentagonais.
ICOSAEDRO
Neste poliedro, os cinco triângulos equiláteros que se encontram em cada vértice, fazem vinte faces. Por isso, o poliedro se chama icosaedro (icosa significa 20 em grego).Este sólido representa a água, porque Platão defendia que a água seria constituída por icosaedros.
CONCLUSÃO
Neste trabalho sobre os sólidos platónicos, concluo que os sólidos têm varias formas e características diferentes, todos eles significam alguma coisa
Bibliografia
I. http://pt.wikipedia.org
II. http://avrinc05.no.sapo.pt/
Subscrever:
Mensagens (Atom)