Cone, cilindro, pirâmide quadrangular, prisma triangular, prisma rectangular, cubo.
quarta-feira, 27 de abril de 2011
Sólidos Platónicos - Trabalho do Eduardo
INTRODUÇÃO
Neste trabalho vou falar nos Sólidos Platónicos, referindo as características de cada um.
Platónicos são sólidos formados por polígonos geometricamente iguais, tendo como sua referencia o filósofo Platão acerca de 350 a.C.
TETRAEDO
CUBO
(hexaedro)
O cubo é o único poliedro regular com faces quadrangulares. O cubo tem 6 faces, pelo que também se pode chamar de hexaedro (hesa significa seis em grego).
Este sólido representa a terra, porque Platão acreditava e afirmava que os átomos de terra seriam cubos, os quais permitiam ser colocados perfeitamente lado a lado, conferindo-lhes solidez.
OCTAEDRO
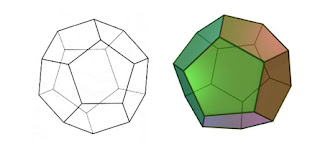
DODECAEDRO
ICOSAEDRO
CONCLUSÃO
Bibliografia
I. http://pt.wikipedia.org
II. http://avrinc05.no.sapo.pt/
Neste trabalho vou falar nos Sólidos Platónicos, referindo as características de cada um.
Platónicos são sólidos formados por polígonos geometricamente iguais, tendo como sua referencia o filósofo Platão acerca de 350 a.C.
TETRAEDO
O tetraedro regular é um sólido platónico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros possui 4 vértices, 4 faces e 6 arestas. Considerado como um caso particular de pirâmide regular de base triangular, o volume do tetraedro regular é dado pela expressão matemática.
O filósofo grego Platão estabelecia uma ligação dos poliedros com as forças da natureza, hoje podemos estudar as formas moleculares existentes na natureza e observarmos que as ideias que Platão teve por volta do século V e IV a.C. são verificadas e comprovadas.
CUBO
(hexaedro)
O cubo é o único poliedro regular com faces quadrangulares. O cubo tem 6 faces, pelo que também se pode chamar de hexaedro (hesa significa seis em grego).
Este sólido representa a terra, porque Platão acreditava e afirmava que os átomos de terra seriam cubos, os quais permitiam ser colocados perfeitamente lado a lado, conferindo-lhes solidez.
OCTAEDRO
O octaedro é um poliedro regular ou sólido platónico. Platão era um filósofo e matemático grego que acabou por se tornar num dos pensadores mais influentes do pensamento ocidental. Nascido em Atenas, cerca de 427 a.C., foi discípulo de Sócrates e uma das ideias que a sua escola de pensamento afirmava era que toda a matéria era constituída por quatro elementos, sendo cada um deles representado por um sólido geométrico regular. Deste modo, fazia corresponder à Terra o cubo, ao Fogo o tetraedro, ao Ar o octaedro e à Água o icosaedro. O dodecaedro foi considerado por Platão como o símbolo do Universo.
DODECAEDRO
O mais harmonioso e soberano dos sólidos Platónicos é o dodecaedro que, segundo Platão, representa o universo ou o cosmos. É constituído por doze pentágonos e não se divide em outros poliedros regulares. Possui 30 arestas, 20 vértices e 12 faces pentagonais.
ICOSAEDRO
Neste poliedro, os cinco triângulos equiláteros que se encontram em cada vértice, fazem vinte faces. Por isso, o poliedro se chama icosaedro (icosa significa 20 em grego).Este sólido representa a água, porque Platão defendia que a água seria constituída por icosaedros.
CONCLUSÃO
Neste trabalho sobre os sólidos platónicos, concluo que os sólidos têm varias formas e características diferentes, todos eles significam alguma coisa
Bibliografia
I. http://pt.wikipedia.org
II. http://avrinc05.no.sapo.pt/
História da Matemática - Trabalho do João Eduardo
Introdução
Neste trabalho vou contar um pouco da História da Matemática. Esta ciência tem uma história muito longa que começa no homem primitivo e que continua até aos nossos dias. Fiz uma pesquisa na internet sobre este tema e encontrei muitas curiosidades sobre a matemática. Procurei também nalguns livros e tirei imagens para mostrar o que encontrei.
A matemática é importante para outras ciências e é muito útil, por isso, o Homem sempre procurou estudá-la e desenvolvê-la. Tentei perceber sobretudo a origem dos números, os sistemas de escrita numérica e a forma como diferentes povos os utilizavam.
Desenvolvimento
Matemática é a “designação genérica das ciências de método essencialmente dedutivo que têm como objecto de estudo os números, figuras geométricas e outras entidades abstractas”. A história da matemática conta a evolução desta ciência e investiga as origens das descobertas matemáticas, assim como dos métodos matemáticos e das notações mais antigas.
Desde o tempo dos homens primitivos, antes da existência da civilização, que encontramos registos de contagem por riscos em pedaços de ossos, pedras e moldes de barro. A nossa civilização começou no chamado período Neolítico (Idade da Pedra Polida) na Mesopotâmia, região situada no Oriente Médio, no vale dos rios Eufrates e Tigre (onde fica actualmente o Iraque), e no Egipto, quando houve um processo de desertificação das florestas. Os homens foram forçados a abandonar a vida nómada (não tinham um sítio fixo para viver) e a fixar-se em aldeias perto dos grandes rios. Começaram a desenvolver técnicas para conseguir produzir alimentos e utensílios e, por isso, precisaram de começar a contar o tempo e, assim, de fazer os primeiros calendários, que os ajudavam a prever as estações, e de ter conhecimentos de astronomia. A numeração escrita nasceu, então, da necessidade de registar o gado ou outros bens, com marcas ou traços em paus, pedras, etc., aplicando o princípio da correspondência biunívoca (a correspondência biunívoca resume-se numa operação de "fazer corresponder"; pode-se dizer que a contagem se realiza fazendo corresponder a cada objecto de um conjunto um número que pertence à sucessão natural: 1,2,3...).
Os sistemas de escrita numérica mais antigos que se conhecem são os dos egípcios e dos babilónios, que datam aproximadamente do ano 3500 a.C..
Os Egípcios
A cultura egípcia desenvolveu-se no noroeste da África, no vale do rio Nilo, desde aproximadamente o ano de 3200 a.C. até aos primeiros séculos da era cristã. Os egípcios desenvolveram três formas de escrita: a mais antiga, usada pelos sacerdotes em monumentos e túmulos, chama-se hieroglífica; desta deriva a escrita usada nos papiros, chamada hierática, da qual resulta, mais tarde, a escrita demótica. Desenvolveram, também, conhecimentos de astronomia e estabeleceram um bom calendário solar feito de doze meses de trinta dias cada um e mais cinco dias de festa no final do ano. Tinham, ainda, profundos conhecimentos de engenharia, pois construíram as pirâmides, imensas estruturas que serviam de túmulos reais. Os egípcios acreditavam numa vida após a morte que dependia da conservação do corpo. Embalsamavam os corpos e guardavam os objectos e valores do dia-a-dia para os colocarem no túmulo para uso depois da morte.
Em 1799, durante as invasões de Napoleão (dirigente francês) no Egipto, engenheiros franceses encontraram um fragmento de pedra que iria ajudar a decifrar a escrita egípcia. Essa pedra (conhecida como Pedra de Roseta) contém inscrições com uma mensagem repetida em hieroglíficos, em caracteres demóticos e em grego. A partir daqui, foi possível decifrar os papiros dos egípcios. Há dois papiros que são as fontes principais de informação sobre a matemática egípcia antiga. O papiro Golonishev ou de Moscou, datado aproximadamente do ano de 1850 a.C., onde encontramos um texto matemático que contém 25 problemas, e o papiro de Rhind (ou Ahmes), datado aproximadamente do ano de 1650 a.C., onde encontramos um texto matemático na forma de manual prático que contém 85 problemas copiados em escrita hierática pelo escriba Ahmes de um trabalho mais antigo. O papiro Rhind descreve os métodos de multiplicação e divisão dos egípcios, o uso que faziam das fracções unitárias, o emprego da regra da falsa posição, a solução para o problema da determinação da área de um círculo e muitas aplicações da matemática a problemas práticos. Todos os 110 problemas incluídos nos papiros de Moscou e de Rhind são numéricos, a maioria tem aplicação prática. Vinte e seis dos 110 problemas dos papiros de Moscou e Rhind são geométricos e de cálculo de áreas de terras e volumes.
O sistema de numeração utilizado pelos egípcios era o sistema de agrupamento simples com base 10. Para os egípcios, um traço vertical valia 1; o número 10 era representado por um osso de calcanhar invertido; o 100 por um laço, e o 1000 por uma flor de lótus. Outros números eram escritos com uma combinação desses símbolos.
Uma parte do papiro Rhind. Depositado no Museu Britânico, Londres.
Os Babilónios
A Mesopotâmia foi inicialmente habitada pelos sumérios, que desenvolveram um sistema de escrita que pode ser o mais antigo da história da humanidade. Eles escreviam usando cunhas em tábuas de argila cozida, dando origem a um tipo de caracteres chamados cuneiformes. Ao longo do tempo, esta região foi invadida por diversos grupos. As antigas civilizações que habitavam a Mesopotâmia são chamadas Babilónios.
Os babilónios tinham conhecimentos matemáticos de álgebra (operações de aritmética) e geometria e faziam cálculos de áreas e volume. Conheciam já o Teorema de Pitágoras (relação matemática entre os três lados de qualquer triângulo rectângulo). Muitos processos aritméticos eram feitos com a ajuda de tábuas.
O sistema de numeração utilizado pelos babilónios era o sistema de agrupamento simples de base 10 para números menores do que sessenta e um sistema posicional que podia ter base 10 ou base 60 para números maiores.
Usavam um traço vertical para representar as unidades e outro desenho para as dezenas:
No sistema decimal, os números de 1 a 99 eram representados por agrupamentos destes símbolos. O símbolo para 100 era composto por traços:
e números superiores a 100, representados novamente por grupos.
Assim, por exemplo, temos:
 Este símbolo indica 10 vezes 100, isto é, 1000. Também usavam, por vezes, o sistema sexagesimal. Os números de 1 a 59 eram representados novamente por agrupamento simples e a partir dali, escreviam-se "grupos de cunhas", com base 60. Os babilónios chegaram a empregar um símbolo, formado por duas cunhas inclinadas, para representar a ausência de um grupo. Como este símbolo não era de uso frequente e nunca foi usado no fim de uma expressão, o sistema babilónio apresentava ambiguidades.
Este símbolo indica 10 vezes 100, isto é, 1000. Também usavam, por vezes, o sistema sexagesimal. Os números de 1 a 59 eram representados novamente por agrupamento simples e a partir dali, escreviam-se "grupos de cunhas", com base 60. Os babilónios chegaram a empregar um símbolo, formado por duas cunhas inclinadas, para representar a ausência de um grupo. Como este símbolo não era de uso frequente e nunca foi usado no fim de uma expressão, o sistema babilónio apresentava ambiguidades.Os Gregos
A história da civilização grega tem as suas origens nas invasões de povos bárbaros na Península Balcânica por volta do segundo milénio a.C.. Estes povos foram conquistando as civilizações ali estabelecidas e avançando em direcção à ilha de Creta. O período histórico da civilização grega teria início por volta de 800 a.C.. Nesta altura os Gregos mudaram do sistema de escrita hieroglífica para o alfabeto fenício. Com o crescente comércio e a necessidade de defesa, o povo grego começou a reunir-se em fortificações, formando a principal unidade política da Grécia Antiga: a cidade-Estado ou polis. Os Gregos espalharam-se por vários pontos do litoral dos Mares Egeu e Negro, chegando a atingir a Bacia do Mediterrâneo e fundaram diversas cidades como Cretona, Elea e Siracusa (cidades da Magna Grécia, no sul da Itália) ou como Mileto e Samos, na Ásia Menor. O grande florescimento da cultura grega surgiu na colónia situada na Ásia Menor, principalmente na cidade de Mileto. No início do século VI a.C., os filósofos de Mileto, entre eles Tales (c. 625 a c. 547 a. C.), começaram a tentar compreender os fenómenos da natureza sem recorrer a mitos e à religião. A utilização do raciocínio dedutivo deu origem à criação de uma matemática dedutiva e formalmente organizada, bem diferente da matemática de carácter prático, desenvolvida no Egipto e na Mesopotâmia.
No final do século IV a.C. o centro do conhecimento e das Matemáticas Gregas mudou-se de Mileto e de outras cidades na Ásia Menor para a Magna Grécia, onde terá vivido Pitágoras (c. 569 a.C. a c. 475 a.C.). Por volta de meados do século V a.C., o centro mudou-se de novo, desta vez para Atenas, onde a matemática e a filosofia se desenvolveram principalmente na Academia de Platão (427 - 347 a.C.).
No final do século IV a.C. o centro do conhecimento e das Matemáticas Gregas mudou-se de Mileto e de outras cidades na Ásia Menor para a Magna Grécia, onde terá vivido Pitágoras (c. 569 a.C. a c. 475 a.C.). Por volta de meados do século V a.C., o centro mudou-se de novo, desta vez para Atenas, onde a matemática e a filosofia se desenvolveram principalmente na Academia de Platão (427 - 347 a.C.).
O maior desenvolvimento da matemática grega deu-se no período helénico, de 300 a.C. a 200 d.C.. Por volta de 300 a.C. o centro da matemática mudou-se de Atenas para a cidade construída por Alexandre, o Grande (358 - 323 a.C.) - Alexandria (no Egipto). Aqui trabalharam matemáticos como Euclides (c. 325 - c. 265 a.C.). Alexandria permaneceu o centro das matemáticas durante cerca de um milénio.
Os textos de maior parte dos matemáticos gregos não chegaram aos nossos dias na sua versão original, uma vez que eram escritos em papiro. Os rolos de papiro eram muito frágeis e com a utilização estragavam-se. Assim, apenas os trabalhos considerados importantes, como os Elementos de Euclides, e que foram copiados frequentemente, chegaram aos nossos dias.
Os Romanos
A civilização romana que, entre os séculos I a.C. e II d.C. ocuparam a Península Ibérica, tinha também um sistema próprio de numeração que, apesar das dificuldades operatórias que apresentava, foi usado na Europa durante muitos séculos e, ainda hoje, é utilizado por nós em várias situações: na designação de papas e reis; na designação de séculos e datas; na indicação de capítulos e volumes de livros; nos mostradores de alguns relógios.
Com o tempo, o sistema de numeração romano sofreu um longo processo de evolução. Inicialmente, os romanos usavam apenas o princípio aditivo (acrescentavam), sendo que um mesmo símbolo podia ser repetido até, no máximo, quatro vezes. Mais tarde, complicaram este sistema, passando a utilizar também o princípio subtractivo, além de permitir a repetição de um mesmo símbolo, no máximo, três vezes.
Sistema de numeração romano
Os Hindus e o sistema de numeração Indo-Arábico ou sistema de numeração decimal
Os hindus, que viviam no vale do Rio Indo, onde hoje é o Paquistão, conseguiram desenvolver um sistema de numeração que reunia as diferentes características dos antigos sistemas. Tratava-se de um sistema posicional decimal. Posicional porque um mesmo símbolo representava valores diferentes, dependendo da posição ocupada; decimal porque eram feitos agrupamentos de dez em dez. Este sistema posicional decimal, criado pelos hindus, corresponde ao nosso actual sistema de numeração. Os árabes foram os responsáveis pela divulgação deste sistema, por isso, designa-se sistema de numeração indo-arábico.
Os dez símbolos utilizados para representar os números denominam-se algarismos indo-arábicos. São eles: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Estes símbolos evoluíram ao longo dos tempos, conforme a seguir se mostra:
Evolução dos símbolos do sistema de numeração indo-arábico.
Este é um sistema preciso que não apresenta ambiguidades porque temos o símbolo 0 (zero) para representar a ausência. A criação de um símbolo para representar o "nada" constitui um dos actos mais importantes da história do pensamento e da matemática. O zero não só permite escrever mais simplesmente os números, como também efectuar operações.
A partir daqui, a história da matemática desenvolveu-se ao longo dos tempos. Na época do Renascimento, uma parte dos textos árabes foram estudados e traduzidos para o latim. A pesquisa matemática concentrou-se, então, na Europa. O cálculo algébrico desenvolveu-se rapidamente com os trabalhos dos franceses Viète e René Descartes. Em seguida, Newton e Leibniz descobriram novas noções matemáticas. Nos séculos XVIII e XIX, a matemática desenvolveu-se bastante com a introdução de novas estruturas abstractas.
Hoje, a matemática é uma ciência que serve de base a muitas outras ciências, como a física, a biologia, a química, etc. e serve as novas tecnologias, como a informática. Podemos perceber como evoluiu a Matemática se pensarmos na primeira contagem do homem primitivo, feita de pequenos traços em ossos e pedras, até aos nossos dias e ao nosso computador pessoal, onde fazemos contas de forma automática.
ANTES
HOJE
Conclusão
Neste trabalho estudei a História da Matemática e os diferentes sistemas de escrita numérica dos povos antigos. Fiquei a saber como o homem primitivo já tentava contar e escrever quantidades e como os Egípcios, os Babilónios, os Gregos e os Romanos desenvolveram esta ciência. Descobri a origem do nosso sistema numérico que se chama indo-arábico.
Gostei de encontrar algumas curiosidades como, por exemplo, a existência do Papiro de Rhind. Neste papiro estão registados vários problemas matemáticos, como este:
Uma quantidade mais a sua quarta parte somam 15; que quantidade é essa?
12 : 4 = 3; 12 + 3 = 15
Este papiro também nos mostra como em 1650 a.C. os Egípcios multiplicavam os números uns pelos outros.
Resolviam problemas como 15 x 16 utilizando o método de duplicar e de somar até chegarem à resposta certa:
1 x 16 ou (1 conjunto de 16) = 16
2 x 16 ou (2 conjuntos de 16) = 32
4 x 16 ou (4 conjuntos de 16) = 64
8 x 16 ou (8 conjuntos de 16) = 128
Tudo junto, isto resulta em 15 conjuntos de 16; logo, se adicionarmos todas as respostas, 15 x 16 = 240.
Bibliografia
Dicionário da Língua Portuguesa, 8ª edição, Porto Editora, 1999.
Snape, Charles e Scott, Heather, Enigmas Matemáticos, Gradiva Júnior, 1994.
http://pt.wikipedia.org/wiki/Hist%C3%B3ria_da_matem%C3%A1tica
http://pt.wikipedia.org/wiki/Hist%C3%B3ria_dos_n%C3%BAmeros_longos
http://www.estudos.de/matematica/HistoriaMatematica/Grecia/MatGrecia.xhtml#preli
http://www.ime.usp.br/~leo/imatica/historia/numeracao.html
http://www.malhatlantica.pt/mathis/grecia/Grecia.htm
http://www.matematicasociety.hpg.ig.com.br/sistema_de_numeracao.htm
http://www.somatematica.com.br/numeros.php
Imagens
http://blog.codefront.net/archives/screenshots/homer-tabbed-browsing.png
http://matematica.no.sapo.pt/cacador.jpg
http://revistagalileu.globo.com/Revista/Galileu2/foto/0,,42299745,00.jpg
http://t1.gstatic.com/images?q=tbn:UFtZvOYDyXInlM:http://i62.photobucket.com/albums/h112/Vania_ch/untitled1.jpg&t=1 (capa)
http://www.ime.usp.br/~leo/imatica/historia/imagens/ht_moscou.gif
http://www.ime.usp.br/~leo/imatica/historia/imagens/ht_prhind.jpg
http://www.matematicasociety.hpg.ig.com.br/sistem3.gif
Sólidos Platónicos - Trabalho do João Eduardo
Introdução
Neste trabalho vou estudar os sólidos geométricos chamados sólidos platónicos. Vou tentar perceber as características geométricas destes sólidos e compreender porque são apenas cinco e porque foram estudados por Platão que lhes deu o nome de platónicos. Vou tentar saber quem foi esta figura e a sua importância para a matemática e outras ciências.
Fiz uma pesquisa na internet sobre este tema e encontrei muitas curiosidades matemáticas sobre o que Platão descobriu e o que pensava ser o significado dos cinco sólidos platónicos. Outros matemáticos também estudaram estes sólidos. Procurei ainda em alguns livros e tirei imagens para ilustrar o que encontrei.
Quem foi Platão?
Platão foi um filósofo (homem que estuda os problemas da existência humana) e matemático do período clássico da Grécia Antiga (cerca 350 a.C.), fundador da primeira Academia de ensino superior do mundo ocidental. Pensa-se que o seu nome verdadeiro tenha sido Arístocles http://pt.wikipedia.org/wiki/Plat%C3%A3o - cite_note-alexander.diogenes.laertius.3.5-14. Platão era um nome que, provavelmente, fazia referência às suas características físicas, como o porte atlético ou os ombros largos, ou ainda a sua excelente capacidade intelectual para tratar diferentes temas.
Platão nasceu em Atenas, provavelmente em 427 a.C., e morreu em 347 a.C.. Quando tinha cerca de 20 anos, conheceu o filósofo Sócrates e tornou-se seu aluno até ele morrer. A sua vida foi dedicada a estudar e a pensar questões filosóficas e tornou se também ele um mestre o que o levou a fundar uma Academia em Atenas. Escreveu textos (diálogos) que eram usados como ferramenta de ensino nas mais diversas disciplinas, como a filosofia, a lógica, a retórica (arte de usar a linguagem para comunicar) e a matemática, entre outras. De entre estes textos, destaca-se Timeu, obra escrita por volta do ano de 350 a.C., na qual Platão demonstra a existência dos chamados sólidos platónicos.
Platão
Sólidos Platónicos
Há um número infinito de diferentes tipos de poliedros (sólidos com faces planas), mas existem apenas cinco que são regulares e que são chamados sólidos platónicos. A sua designação foi atribuída por Platão, que os descobriu cerca de 400 a.C.. Os sólidos platónicos são poliedros – sólidos cujas faces têm a forma de polígonos – regulares – todas as faces são polígonos geometricamente iguais (chamam-se congruentes) – e todos os seus ângulos são também congruentes. Assim, um poliedro regular tem todas as suas faces congruentes, todas as suas arestas idênticas e todos os seus ângulos iguais. A existência destes sólidos já era conhecida anteriormente pelos pitagóricos (da escola de Pitágoras de Samos que foi um filósofo e matemático grego que nasceu em Samos, entre cerca de 570 a.C. e 571 a.C.) e os egípcios utilizaram alguns deles na arquitectura e noutros objectos que construíram, mas foi Platão quem observou melhor esta característica. Por isso se chamam platónicos. Platão estudou estes sólidos e demonstrou que eram os únicos sólidos com as faces todas iguais.
Os sólidos platónicos são apenas cinco: o tetraedro, o cubo, o octaedro, o dodecaedro e o icosaedro.
Num dos textos incluído no diálogo Timeu, Platão demonstrou que são apenas cinco os sólidos platónicos através da sua construção e utilizando apenas polígonos geometricamente iguais.
Assim, com triângulos equiláteros só se consegue construir o tetraedro, o octaedro e o icosaedro.
Com o quadrado, se tentarmos construir um sólido com as faces geometricamente iguais, apenas conseguimos o cubo. Com pentágonos, apenas conseguimos construir o dodecaedro.
Com hexágonos já não se consegue construir nenhum sólido platónico.
Por isso, podemos verificar que são apenas cinco os sólidos que se podem construir a partir de polígonos geometricamente iguais: o tetraedro, o octaedro, o icosaedro, o cubo e o dodecaedro. São precisamente cinco, como se queria demonstrar.
Platão tentou encontrar um significado para esta curiosidade e por isso desenvolveu uma teoria segundo a qual os quatro "elementos" - o fogo, o ar, a água e a terra - eram todos sólidos minúsculos. Platão defendia que, uma vez que o mundo só poderia ter sido feito a partir de corpos perfeitos, estes elementos deveriam ter a forma de sólidos regulares:
o fogo era o mais leve e o mais violento dos elementos, por isso deveria ser um tetraedro;
a terra era o elemento mais estável, deveria ser o cubo;
a água, o elemento mais inconstante e fluído, era um icosaedro, o sólido regular capaz de rolar mais facilmente;
quanto ao ar, Platão observou que "o ar é para a água o que a água é para o ar," e concluiu, de forma um pouco misteriosa, que o ar deve ser um octaedro;
por último e para incluir o quinto sólido regular, atribuiu ao dodecaedro a representação da forma de todo o universo.
Também Johannes Kepler (1571-1630), que foi um astrónomo, matemático e astrólogo alemão e uma importante figura da revolução científica do século XVII, tentou explicar os movimentos planetários a partir dos sólidos platónicos e interpretou, na sua obra Harmonices Mundi, as associações de Platão da seguinte forma:
Outra forma de demonstrar que existem apenas cinco sólidos platónicos é através da fórmula de Euler. Leonhard Paul Euler (1707 -1783) foi um matemático e físico suíço de língua alemã que fez importantes descobertas em várias áreas e também para a matemática moderna. Euler considerou o número de vértices, de arestas e de faces de cada um dos sólidos platónicos e encontrou a seguinte fórmula: V + F - A = 2 (ou V + F = A + 2), onde V, F e A são, respectivamente, o número de vértices, faces e arestas do poliedro. Euler descobriu-a em 1750 e fez muitas verificações da sua ideia, para diversos tipos de sólidos, mas não apresentou nenhuma demonstração, dizendo o seguinte:
"Devo admitir em primeiro lugar que ainda não consegui uma demonstração rigorosa deste teorema... Como, em todo o caso, a sua verdade foi estabelecida em tantos casos, não pode haver dúvidas que é verdadeiro para qualquer sólido. Portanto a proposição parece satisfatoriamente demonstrada".
Mais tarde, Euler acabou por apresentar uma demonstração. Para Euler, o teorema aplicar-se-ia a todos os poliedros. No entanto, vários matemáticos atacaram essa ideia, o que originou uma grande discussão à volta deste teorema, levando a sucessivas demonstrações e a contradizer a sua validade, com base na descoberta de poliedros que não confirmavam a teoria.
Todos os sólidos platónicos satisfazem a relação:
vértices + faces = arestas + 2
como se pode ver na seguinte tabela:
Uma curiosidade é que os sólidos platónicos têm a seguinte coincidência quando os agrupamos: o cubo tem seis faces e oito vértices e o octaedro tem oito faces e seis vértices; o dodecaedro tem doze faces e vinte vértices e o icosaedro tem vinte faces e doze vértices; o tetraedro fica sozinho mas tem o mesmo número de faces e de vértices (quatro).
Conclusão
Neste trabalho estudei os sólidos platónicos e descobri como são geometricamente iguais. Estes sólidos, que são apenas cinco, têm todas as suas faces congruentes, todas as suas arestas idênticas e todos os seus ângulos iguais. Platão, que foi um importante filósofo grego, descobriu estes sólidos e demonstrou que eram apenas cinco os que tinham estas características. Por isso, Platão tentou explicar uma teoria através dos elementos da Natureza. Fiquei também a conhecer outros importantes matemáticos e como estudaram os sólidos platónicos, encontrando regras matemáticas e fórmulas para explicar a sua forma.
Gostei de encontrar a explicação da existência entre a Natureza e estes sólidos e de ficar a saber um pouco da história de Platão, como por exemplo, a Academia que ele fundou e que foi a primeira escola de ensino superior e que tinha escrito na entrada:
“não entre ninguém que não saiba geometria”.
Bibliografia
Dicionário da Língua Portuguesa, 8ª edição, Porto Editora, 1999.
Conceição, Alexandra, Almeida, Matilde, Conceição, Cristina e Costa, Rita, Matemática sob Investigação – 5º ano, parte 1, Areal Editores.
Pappas, Theoni, Fascínios da Matemática, A descoberta da matemática que nos rodeia, Editora Replicação, 1995.
Pereira, Maria Helena da Rocha, Estudos de História da Cultura Clássica, 5ª edição, Fundação Calouste Gulbenkian, 1980.
Wells, David, Dicionário de Geometria Curiosa, Gradiva, 1991.
http://pt.wikipedia.org/wiki/Filosofia
http://pt.wikipedia.org/wiki/Johannes_Kepler
http://pt.wikipedia.org/wiki/Pitágoras
http://pt.wikipedia.org/wiki/Platão
http://sempreamathematicarcommusica.blogspot.com/2010/10/solidos-geometricos.html
http://www.educ.fc.ul.pt/icm/icm99/icm43/sol_plat.htm
http://www.google.com/search?q=timeu&ie=utf-8&oe=utf-8&aq=t&rls=org.mozilla:pt-BR:official&client=firefox-a
Imagens
http://cmup.fc.up.pt/cmup/pick/Manhas/PoliedrosPlatao2.jpg
http://farm1.static.flickr.com/94/280790074_84adcbed6f.jpg (capa)
http://www.lutalivresubmission.com.br/imgs/platao.jpg
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgN2h7rKRMwYgksqJEQz3ePvLyA4AuC_GsInADFzi5gLV_k_F8c6WmGM3KpIefE7cOrkAY-Q9R9aFnTdK5E65ov9fmxgPRW828B7XRb785ToI4SPOBiFN3hRupKVCVdaprgHX3CWJsolLjf/s320/elementos+da+natureza.jpg
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh3O7tAPPZEqG7TYh1uXczwxATrpvdIV-LydHARdi0AWxPT57GEFzZUaIPsXdI4PYQOhHqilYXqzUnYY1u6_XsIaRgKKCSiuYXw0AuuQaed7fG8l-W64ymY4uA-_WHTXOZoFpfTijsvO5A3/s1600/6.jpg
Subscrever:
Comentários (Atom)